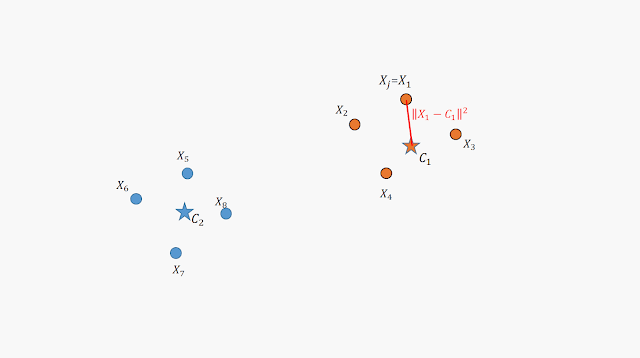
此方法利用了隸屬值member ship value與 fuzzier "m" 來進行模糊化,描述了樣本屬於哪個類別,與樣本的隸屬程度,類似機率的概念,我們用圖形來解釋公式。
上圖共有 8 個數據點,分別為 X1 ~ X8 ;以及兩個群心(Center of cluster) C1、C2 。
對於數據點我們用 Xj 來表示第 j 個 ; 群心(質心)則用 Ci 來表示第 i 個
上圖說明了這八個數據點與群心之間的關係,我們用隸屬值(Menbership value) 來判定數據點屬於 C1 類還是 C2 類。一個群心會對所有的數據點都產生一個隸屬值,反過來說,當我們有兩個群心時,同一個數據點就會具有兩個隸屬值(以此類推至三個群 .. 四個群 ...)
對於 C2 群心也是,每一個數據點都會有其對應的隸屬值。注意 uij 的念法為 " 第 j 個數據點對第 i 個群心的隸屬值 "
因為隸屬值又帶有機率的概念,所以我們定義對於單一個數據點而言,其所具有的隸屬值加總為 " 1 " 。
隸屬值講完了我們來看看距離。距離的概念在 K-means 的地方也有,由上圖中我們可以得到各個數據點到群心的距離。
FCM 的群心是藉由 "所有的數據點" 以 "距離乘上隸屬值" 而成。所以 C1 可以有上圖中的表示式,值得注意的是在隸屬值的地方出現了次冪 m ,此值稱為 fuzzier ,就是 FCM 中的 Fuzzy ,此值可以調控該項對於群心計算的影響力。
上圖具有兩個觀念
一、
比較上圖與上上圖,我們發現 C1 群心的計算可以有一個近似條件。這樣想好了,如果我們要計算 C1 的群心位置,常理來說就應該用屬於 C1 類的數據點來進行計算,但在上上圖中我們提到 FCM 的群心是所有數據點皆有貢獻,顯然不符合我們所說的常理,所幸的是對於 C1 群心而言, X5~X6 對應的隸屬值都會變的很小(藉由疊代的過程)所以可以被忽略。
二、
由(一)所提及的觀念,我們可以得出 C1 應該要由 X1~X4 並乘上其對應的隸屬值計算而成;同理 C2 應該要由 X5~X6 並乘上其對應的隸屬值而成。
接著我們思考,要如何去衡量 FCM 的聚類成效如何? 最直關的想法就是屬於 C1 類的數據點全部都擠在 C1 群心;屬於 C2 類的數據點都權擠在 C2 群心。而全部擠在一起代表著距離為 " 0 " ,故我們可以將 C1 的群心計算與 C2 的群心計算合併在一起寫成 Objective function J ,並且認為這個值越小越好。
由高中數學得知,要取得一個函數的極大值(極小值)只要求其導數並令為零就可以。但 Objective function J 還被另一個限制條件框住,也就是先前提到的單一數據點的隸屬值總和為零。
所以我們用了拉格朗日的技巧來解決這個問題。詳細過程請參閱參考連結,在這我們得到兩個結果分別為隸屬值 uij 以及群心 Ci
我們將隸屬值的結果拿來看,這個公式很有趣是可以用物理(?)的角度來進行解釋的。
假設 m=2, k=2, i=j=1 ,則 X1 對於群心 C1 的隸屬值為上式。由上式我們發現這屬於一個分餅的概念,也就是說對於X1 對於群心 C1 的隸屬值而言,是藉由 X1 至 C1 以及 C2 距離分之 C1 距離而得到的,在公式中出現了倒數的原因可參見上圖內的文字說明。
同樣的群心 C1 的計算也有分餅的概念存在,其結果為各數據點對 C1 的隸屬值平方加總分之第 j 個數據點的隸屬值平方再乘上數據點的值。
最後給上程序的流程圖為以上
clc
clear
close all
%% create samples:
for i=1:100
x1(i) = rand()*5;
y1(i) = rand()*5;
x2(i) = rand()*5 + 3;
y2(i) = rand()*5 + 3;
end
x = [x1,x2];
y = [y1,y2];
data = [x;y];
data = data';
figure
plot(data(:,1),data(:,2),'k*');
%% ---
cluster_n = 2; %類別數量
iter = 100; % 疊代停止次數
m = 2; % fuzzier
num_data = size(data,1);%樣本個數
num_d = size(data,2);%樣本維度
% --初始化隸屬值uij,且含限制條件
U = rand(cluster_n,num_data);
col_sum = sum(U);
U = U./col_sum(ones(cluster_n,1),:);
%%
for i = 1:iter
% 更新 Ci
for j = 1:cluster_n
u_ij_m = U(j,:).^m;
sum_u_ij = sum(u_ij_m);
c(j,:) = u_ij_m*data./sum_u_ij;
end
% 更新 uij
for j = 1:cluster_n
for k = 1:num_data
sum1 = 0;
for j1 = 1:cluster_n
temp = (norm(data(k,:)-c(j,:))/norm(data(k,:)-c(j1,:))).^(2/(m-1));
sum1 = sum1 + temp;
end
U(j,k) = 1./sum1;
end
end
% 計算目標函數 J
temp1 = zeros(cluster_n,num_data);
for j = 1:cluster_n
for k = 1:num_data
temp1(j,k) = U(j,k)^m*(norm(data(k,:)-c(j,:)))^2;
end
end
J(i) = sum(sum(temp1));
end
%% 繪圖
figure;
plot(J);
figure
hold on
[~,label] = max(U); % 找到所屬的類
gscatter(data(:,1),data(:,2),label)
plot(c(:,1),c(:,2),'kd')
參考連結
MATLAB自带的FCM算法整合整理
聚類之詳解FCM算法原理及應用
Fuzzy C-Means Clustering - Objective Function
Fuzzy C-Means Clustering - Minimization of Objective Function I
Fuzzy C-Means Clustering - Minimization of Objective Function II
A Tutorial on Clustering Algorithms - Fuzzy C-Means Clustering