以台灣的歷年總人口數舉例,就屬於一個離散性的資料,例如民國35年人口數為6090860;民國36年人口數為6497734 ... 以此類推。假若我們今天想要知道35.5年的人口數是多少呢?聰明的你可能會把兩個年份的人口數加總並且平均,事實上這就是線性內插(linear interpolation)的方法,將兩個年份的資料點用直線相連,自然的在35.5年處就會是兩個年份的平均值了。
在MATLAB裡面可以很容易的實現線性內插的方法,使用指令 interp1
% 線性內插
figure
hold on
plot(data_year,data_people,'o')
interp_index = 35:0.5:106;
linear_interp = interp1(data_year,data_people,interp_index);
plot(interp_index,linear_interp)
title('台灣歷年總人口數')
xlabel('年(民國)')
ylabel('人口數')
set(findall(gcf,'type','axes'),'fontsize',10, 'fontname' , '標楷體')
set(findall(gcf,'type','text'),'fontsize',10, 'fontname' , '標楷體')
在離散數據變動較大的時候,線性內插的效果往往不符合需求,這時我們需要別的內插方法。例如曲線內插(spline interpolation)或是立方內插(cubic interpolation)
% 曲線內插
figure
hold on
plot(data_year,data_people,'o')
interp_index = 35:0.5:106;
linear_interp = interp1(data_year,data_people,interp_index,'spline');
plot(interp_index,linear_interp)
title('台灣歷年總人口數(曲線內插)')
xlabel('年(民國)')
ylabel('人口數')
set(findall(gcf,'type','axes'),'fontsize',10, 'fontname' , '標楷體')
set(findall(gcf,'type','text'),'fontsize',10, 'fontname' , '標楷體')
% 立方內插
figure
hold on
plot(data_year,data_people,'o')
interp_index = 35:0.5:106;
linear_interp = interp1(data_year,data_people,interp_index,'cubic');
plot(interp_index,linear_interp)
title('台灣歷年總人口數(立方內插)')
xlabel('年(民國)')
ylabel('人口數')
set(findall(gcf,'type','axes'),'fontsize',10, 'fontname' , '標楷體')
set(findall(gcf,'type','text'),'fontsize',10, 'fontname' , '標楷體')
因人口總數的變動很小,故三種內插法事實上效果都相同,在此範例中僅做為註記用法使用。
接著我們介紹迴歸分析,在本章中介紹的是"線性"迴歸且基於"曲線擬合(Curve Fitting)"來建立數學模型,以幫助我們在建立數學模型後來進行未來數據的預測。而曲線擬合所建出來的數學模型為一個SISO系統;"曲面擬合(Surface Fitting)"則是針對MISO系統。
無論是曲線擬合或是曲面擬合,在資料分析上都稱為迴歸分析(Regression Analysis)
這麼說起來或許有點難懂,讓我們先將問題簡化。如果有一個離散的資料組,如下圖,那我們能不能用一條直線(或多項式)來對這些離散資料進行數學建模? 又文言了,事實上,數學建模的意思我們可以理解為 "用一個數學的方程式(或專業一點稱為模型)企圖用來代表這些數據點" ,而其跟深刻的用意(或說科學家想做的)是透過數學建模的動作,我們就可以直接利用這些方程式來預測(或研究),例如用數學建模一顆飛彈,我們就可以利用這個方程式在電腦上直接模擬這顆飛彈的飛行軌道,而不用真正射出一顆飛彈。
扯遠了,總之用一條直線(或多項式)來代表數據組,這樣的概念就是迴歸分析,且屬於曲線擬合(single input single output, SISO系統)
為了驗證預測的準確度,在迴歸分析的部分我取用民國35到100年的數據,並利用模型預測105年的人口數,藉此來比對預測的效果如何。以下列表為官方資料統計結果
民國 人口數
... ...
100 23224912
101 23315822
102 23373517
103 23433753
104 23492074
105 23539816
Matlab 自帶函數 polyfit 可以執行基於"最小平方法"的多項式迴歸,什麼是最小平方法呢? 事實上我們可以先思考,該怎樣用一條直線來代表這四個數據組? 數學家就想到一個方法,其原理說穿了也頗好理解的,也就是找出某一條直線,且這一條直線與四個數據點的絕對距離合最小。若有點難以理解這句話,我們利用 y = ax+b 的一次多項式來理解。
有四個數據點分別為數據點1、數據點2 ... ,並且我們假設想要利用一條直線來代表這四個數據點(紅線),數據點1到這條紅線的距離為d1,其他數據點以此類推。若要計算這四個點到這條直線的距離合(也就是d1+d2+d3+d4),最直觀的就是取絕對值。但當年覺得取絕對值太麻煩了不利於計算(個人瞎猜),所以將距離進行平方後相加,以避免距離為負值的影響。
而這是背後的原理,知道即可,事實上 Matlab 已經幫我們處理好這麻煩的部分。
%% 一次線性迴歸(Regression1)
figure
hold on
plot(data_year_100,data_people_100,'o')
parmeter1 = polyfit(data_year_100,data_people_100,1)
index = 35:0.1:110;
Regression1 = polyval([parmeter1(1),parmeter1(2)],index);
plot(index,Regression1)
title('台灣歷年總人口數(一次線性迴歸)')
xlabel('年(民國)')
ylabel('人口數')
set(findall(gcf,'type','axes'),'fontsize',10, 'fontname' , '標楷體')
set(findall(gcf,'type','text'),'fontsize',10, 'fontname' , '標楷體')
polyfit函數的第三個參數即為上方方程式中的n,n = 1 代表的就是一次多項式,也就是 y=ax+b的形式。其結果會回傳兩個參數(更正確的說,是回傳n+1個參數),也就是說我們要的 a 跟 b了。接著利用index為polyval進行索引,polyval其輸入為方程式的係數(詳見參考連結),故意設到110(代表民國110年)用以預測,最後畫出該回歸方程。
parmeter1 =
1.0e+06 *
0.2801 -2.5545
意謂著 a = 1.0e+06 *0.2801 , b = 1.0e+06 *(-2.5545) 即 y = (1.0e+06 *0.2801)x - 1.0e+06 *2.5545
我們可以看出一次多項式根本沒辦法用來代表台灣歷年人口的數據組,想想其實也合理,畢竟人口不太可能是線性成長的,於是我們將 n 提高,並且比較到 n = 4 來看看效果如何。
%% 二三四次線性迴歸(Regression2、Regression3、Regression4)
hold on
plot(data_year_100,data_people_100,'o')
parmeter2 = polyfit(data_year_100,data_people_100,2)
parmeter3 = polyfit(data_year_100,data_people_100,3)
parmeter4 = polyfit(data_year_100,data_people_100,4)
index = 35:0.1:110;
Regression2 = polyval([parmeter2(1),parmeter2(2),parmeter2(3)],index);
Regression3 = polyval([parmeter3(1),parmeter3(2),parmeter3(3),parmeter3(4)],index);
Regression4 = polyval([parmeter4(1),parmeter4(2),parmeter4(3),parmeter4(4),parmeter4(5)],index);
plot(index,Regression2,index,Regression3,index,Regression4)
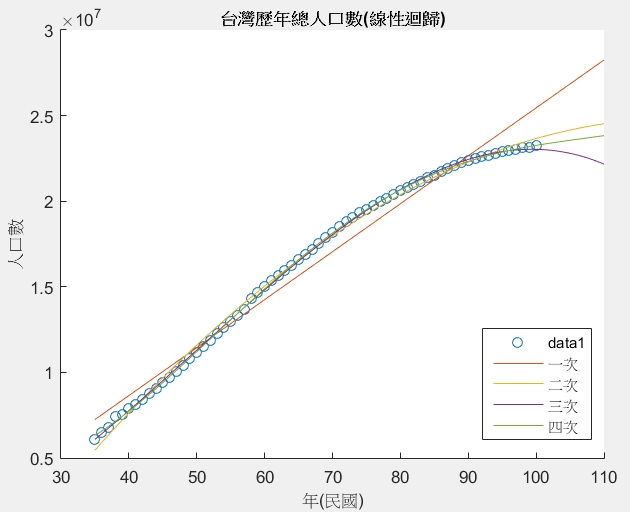
title('台灣歷年總人口數(線性迴歸)')
xlabel('年(民國)')
ylabel('人口數')
set(findall(gcf,'type','axes'),'fontsize',10, 'fontname' , '標楷體')
set(findall(gcf,'type','text'),'fontsize',10, 'fontname' , '標楷體')
最後我們利用polyval來取得四個擬合出來的多項式曲線對於105年的預測,並且與實際值進行比較,以百分比的方式來計算出誤差量。如下
人口數 誤差百分比( (預測值-實際值)/實際值 )
實際值 23539816 none
一次擬合 26851683 14.17 %
二次擬合 24157599 2.62 %
三次擬合 22796090 -3.15 %
四次擬合 23558641 0.08 %
由此可知四次擬合的準確度可以說是非常精良的,覺得神奇嗎!? 讓我們看看110年的四次擬合預測台灣總人口數是多少。其結果為23831032人,五年多了29萬人,平均人口年成長率為0.25% !? 啊 .. 是我對於平均人口年成長率的算法錯誤嗎? 針對台灣的人口數未來擔憂啊 ...
Regression1_105 = polyval([parmeter1(1),parmeter1(2)],105)
Regression2_105 = polyval([parmeter2(1),parmeter2(2),parmeter2(3)],105)
Regression3_105 = polyval([parmeter3(1),parmeter3(2),parmeter3(3),parmeter3(4)],105)
Regression4_105 = polyval([parmeter4(1),parmeter4(2),parmeter4(3),parmeter4(4),parmeter4(5)],105)
但大家有沒有發現一個問題? 若我們沒有105年的精準人口統計數字可以看出四次擬合的預測結果最為優秀,那我們要如何確定四次擬合才是我們要的呢? 為什麼 n 不選擇 5、6、7 ?(事實上若階數過高可能會發生"過擬合"的問題,反而會讓預測值不準)
實際上polyval() 函數回傳的值可以取得殘差(residual)的資訊。殘差分析是指迴歸分析中,針對預測誤差(或稱作估計誤差)所進行的分析。殘差值則是指觀察值與預測值之間的差距,總而言之殘差值越小,代表越精準就是。
將十個擬合的多項式殘差值進行提取,列表如下
殘差值(10^6)
一次擬合 7.1984
二次擬合 2.3409
三次擬合 0.9836
四次擬合 0.6628
五次擬合 0.6616
六次擬合 0.5278
七次擬合 0.4604
八次擬合 0.4588
九次擬合 0.4474
十次擬合 0.4451
for i = 1:10
[P S]=polyfit(data_year_100,data_people_100,i)
S1(i) = S.normr
end
figure
plot(S1)
title('殘差估計')
xlabel('階數n')
ylabel('殘差值')
可以看的出來,階數越高殘差越小,但在 n > 6 之後基本上已經沒什麼區別。由於前述有提到當階數 n 使用過高時會有過擬合的問題,故在使用上還是夠用就好,沒有必要硬要挑殘差最低的階數來進行擬合。
本文參考以下三個連結
10-1 線性迴歸:曲線擬合
MATLAB 之工程應用:11.13 迴歸分析regress
MATLAB 曲線配適(迴歸)與內插
維基百科