本文主要從一階電路 RC低通濾波器(Low-pass filter)的轉移函式開始推導,並分析其波德圖。
目標為對一個具有 50Hz 以及 700Hz 的輸入訊號進行低通濾波,嘗試濾除訊號中的高頻成份(700Hz)。
推導的結果如上圖,輸入為Vin、輸出為 Vout 以及轉移函式 H(s)。其中該 RC 電路的轉移函式就是一個低通濾波器,在此我們先假設 R*C 為 2,由此就可以推導出截止頻率(Cut-off frequency)為 1/RC = 0.5(rad/sec) 若以頻率來說就是 0.5/2pi (Hz)。近似波德圖(頻率響應圖)如右上角所示,直接由截止頻率對應的 -3dB 點來驗證是否正確。
由右下角的實際波德圖(MATLAB 對轉移函式取 bode plot)可以看出,在 -3dB 點的地方確實對應到的是 0.5 (rad/sec) 。
下圖:故我們就可以直接更改 MATLAB 程式碼,直接更改轉移函式分母項原本為 2 的地方, 更改為 0.0032 ,就可以設計截止頻率為 50Hz (R*C = 0.0032),如此一來就有了我們需要的低通濾波器(頻域)。
註:波德圖的大小圖,其單位為 dB ,也就是說假設訊號在該頻率衰減了 3dB,經由計算 20log(X) = -3dB,可以得到原始訊號在該頻率衰弱了 0.707 倍。
接著是產生我們所需要的輸入訊號,也就是一個具有 50Hz 以及 700 Hz 成份的訊號。
直接進行快速複利葉轉換進行頻譜分析(NFFT = N),由最下方的圖可以看出確實是 50Hz 以及 700Hz 的加總訊號( 頻率為50Hz振幅為 10 的訊號 + 頻率為10Hz振幅為 1 的訊號)
由於 Matlab 若要進行下一步(將離散訊號進行濾波),必須要將我們的低通濾波器(頻域)轉換為離散型式,如此一來有點繞太遠了,故我們先利用 PSIM (一個專門用來針對電力電子進行模擬的軟件) 來進行簡單的結果展示,先看結果,再回頭過來用 Matlab 實現,交叉比對。
PSIM 支援直接使用 Low-pass 方塊來進行訊號的濾波。由上圖可以看出,藍色濾波後的訊號明顯出現了振幅上的衰減以及相位的延遲,振幅上的衰減在時域圖比較不好分辨,但可以由下方的頻譜分析圖看出來, 由於我們的截止頻率就恰巧設計在 50 Hz 的地方,這會導致在截止頻率(50Hz)的原訊號產生 -3dB( 10*0.707倍 = 7.07 )的衰減,而 10倍頻外的 700 Hz,幾乎完全消失,由上述可以確定 PSIM 的結果無誤,故我們現在的任務就是利用 Matlab 的濾波器,將時域訊號的結果與上圖比對,若符合則代表成功 (還有一個要回頭使用 Matlab的原因是,我在 PSIM 中找不到可以很好的將其設計結果轉變為 C 語言撰寫的方法,但這問題在下一章得到解決) 。
回到 Matlab,如前述,我們現在需要的是將位於頻域的 Low-pass filter 轉到 Z- domain 下。Matlab 支援直接將頻域轉移函式轉換為離散域轉移函式,如此一來我們就可以得到差分方成的係數,就可以用 C 語言進行實現了。在 Matlab 使用的函式為 c2d(signal,sampletime,['Method',' ']),結果圖如下( 程式碼的部分放在文末一併給出)
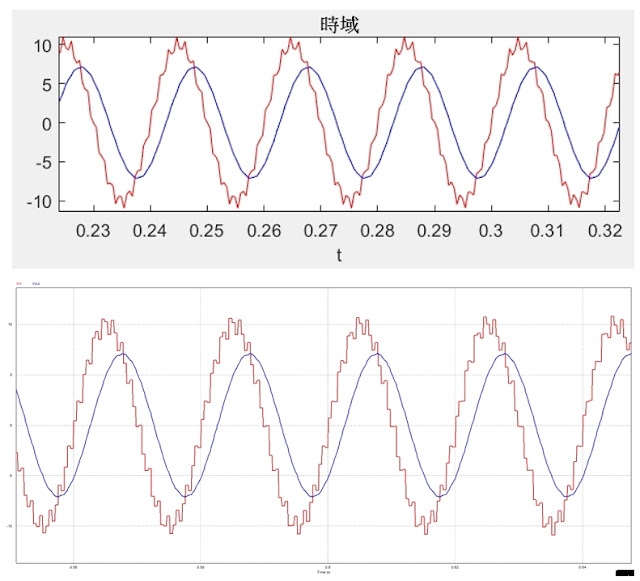
由頻譜分析可以看出是對的。將 Matlab(上) 跑出來的與 PSIM(下) 交叉比對,感受的出來有模有樣啊 !
求取出來的 Low pass in Z-Domain
有了 Low pass in Z-domain 表達式,就可以轉為差分方程用 C 語言實現。然而除了實現以外,在本篇中還缺少了一個重要的概念那就是"延時(遲)",待下篇分曉。
% http://wyj-learning.blogspot.tw/2017/08/matlab-rc-low-pass.html
clc
clear all
close all
% 建立 H(s)轉移函式
R = 1
C = 2
num = [1] % 分子多項式係數
den = [R*C 1] % 分母多項式係數
Hs = tf (num,den)
% 極零點圖
% pzmap(Hs)
% Bode plot
figure
bode(Hs)
grid on
% 建立 input ( 50Hz sin函數 + 700Hz sin函數)
fs = 2048
Ts = 1/fs
N = 1024
n = [0:1:N-1];
freq_resolution = fs/N % 解析度太低-> N上升
t=n/fs;
f1 = 50;
f2 = 700;
input = 10*sin(2*pi*f1*t) + 1*sin(2*pi*f2*t);
figure
subplot(2,1,1);
plot(t,input)
title('時域')
xlabel('t');
axis tight
% 頻譜分析
NFFT = N
Y = fft(input,NFFT); % Spectrum
mag=abs(Y);
subplot(2,1,2);
f=n*fs/NFFT; % n*fs/NFFT,若要提高fft頻率範圍僅有提升fs(in this case)
plot(f(1:NFFT/2),mag(1:NFFT/2)*2/NFFT,'-b');
grid on
xlabel('Frequency(Hz)');
ylabel('Magnitude');
title('FFT of signal');
axis([-inf,inf,0,15])
%% 1st-order low pass ( cut-off freq. = 50Hz )
RC = 1/(2*pi*50)
num = [1] % 分子多項式係數
den = [RC 1] % 分母多項式係數
Hs_1 = tf (num,den)
% 極零點圖
%pzmap(Hs_1)
% Bode plot
figure
bode(Hs_1)
title('Bode plot (Cut-off freq. = 50Hz)')
grid on
%% 濾波器離散化
sample_time = Ts
sysd1 = c2d(Hs_1, sample_time) % 方法默認為zoh法、濾波器大多採用'imp'、控制器大多採用'tustin'
%opt = c2dOptions('Method', 'tustin');
%sysd1 = c2d(Hs_1, sample_time, opt)
sysd1_num = sysd1.num{1} % 分子
sysd1_den = sysd1.den{1} % 分母
% 濾波
filter_input = filter(sysd1_num,sysd1_den,input);
% input t域
subplot(2,1,1);
plot(t,filter_input);
xlabel('t(sec)');
title('時域')
axis tight
% 頻譜分析
NFFT = N
filter_Y = fft(filter_input,NFFT); % Spectrum, NFFT = 1024
filter_mag=abs(filter_Y);
subplot(2,1,2);
f=(0:NFFT-1)*fs/NFFT;
plot(f(1:NFFT/2),filter_mag(1:NFFT/2)*2/NFFT,'-b');
grid on
xlabel('Frequency(Hz)');
ylabel('Magnitude');
title('FFT of signal');
axis([-inf,inf,0,15])
%% 結果比較
figure
subplot(2,1,1);
plot(t,input,'-r',t,filter_input,'-b')
title('時域')
xlabel('t');
axis tight
subplot(2,1,2);
plot(f(1:NFFT/2),mag(1:NFFT/2)*2/NFFT,'-r',f(1:NFFT/2),filter_mag(1:NFFT/2)*2/NFFT,'-b');
grid on
xlabel('Frequency(Hz)');
ylabel('Magnitude');
title('FFT of signal');
axis([-inf,inf,0,15])






